Introduction
This section lists some examples of shifts in the Good Market Equilibrium as well as the labor market equilibrium.
Additionally, I am leaving my tikz code– these provide decent examples for making these kinds of graphs.
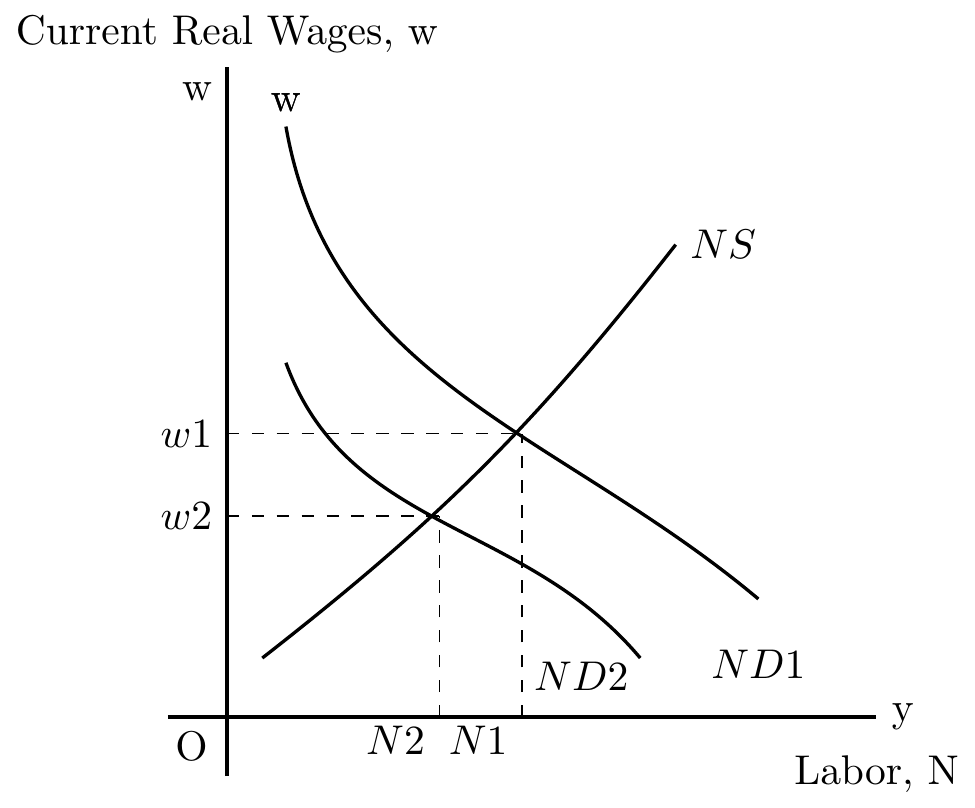
Supply Shock Example
Imagine the cost of energy increasing.
This rising cost would make each worker less productive at any level of output (supply side shock).
This subsequent reduction of the marginal product of labor would shift the equilibrium such that firms would require less workers in order to achieve equilibirium.
\begin{tikzpicture}[scale=1]
% Axis
\draw [thick] (-0.3,0) node [below] {O} (-0.5,0)-- (0,0) -- (5.5,0) node [right] {y};
\node [above] at (0,5.5) {Current Real Wages, w};
\node [below] at (5.5,-0.2) {Labor, N};
\draw [thick] (0,-0.5)-- (0,0) -- (0,5.5);
\node [left] at (0,5.3) {w};
%Downward slopping line
\node [above] at (0.5,5) {w};
\draw [thick] (0.5,5) to [out=280,in=140] (4.5,1);
\node [above] at (4.5,0.2) {$ND1$};
%Downward slopping line after shock
\node [above] at (0.5,5) {w};
\draw [thick] (0.5,3) to [out=290,in=130] (3.5,.5);
\node [above] at (3,0.1) {$ND2$};
% Upward Slopping PQ
\draw [thick] (0.3,0.5) to [out=38,in=232] (3.8,4);
\node [left] at (0.43,0.5) {};
\node [right] at (3.8,4) {$NS$};
% dashed lines
\draw [dashed] (0,2.4)--(2.5,2.4);
\node [left] at (2.5,-.2) {$N1$};
% New Equilibrium
\draw [dashed](1.8,0)--(1.8,1.7);
% Old Equilibrium
\draw [dashed](2.5,0)--(2.5,2.4);
\draw [dashed](0,1.7)--(1.8,1.7);
\node [left] at (1.8,-.2) {$N2$};
\node [left] at (0,1.7) {$w2$};
\node [left] at (0,2.4) {$w1$};
\end{tikzpicture}
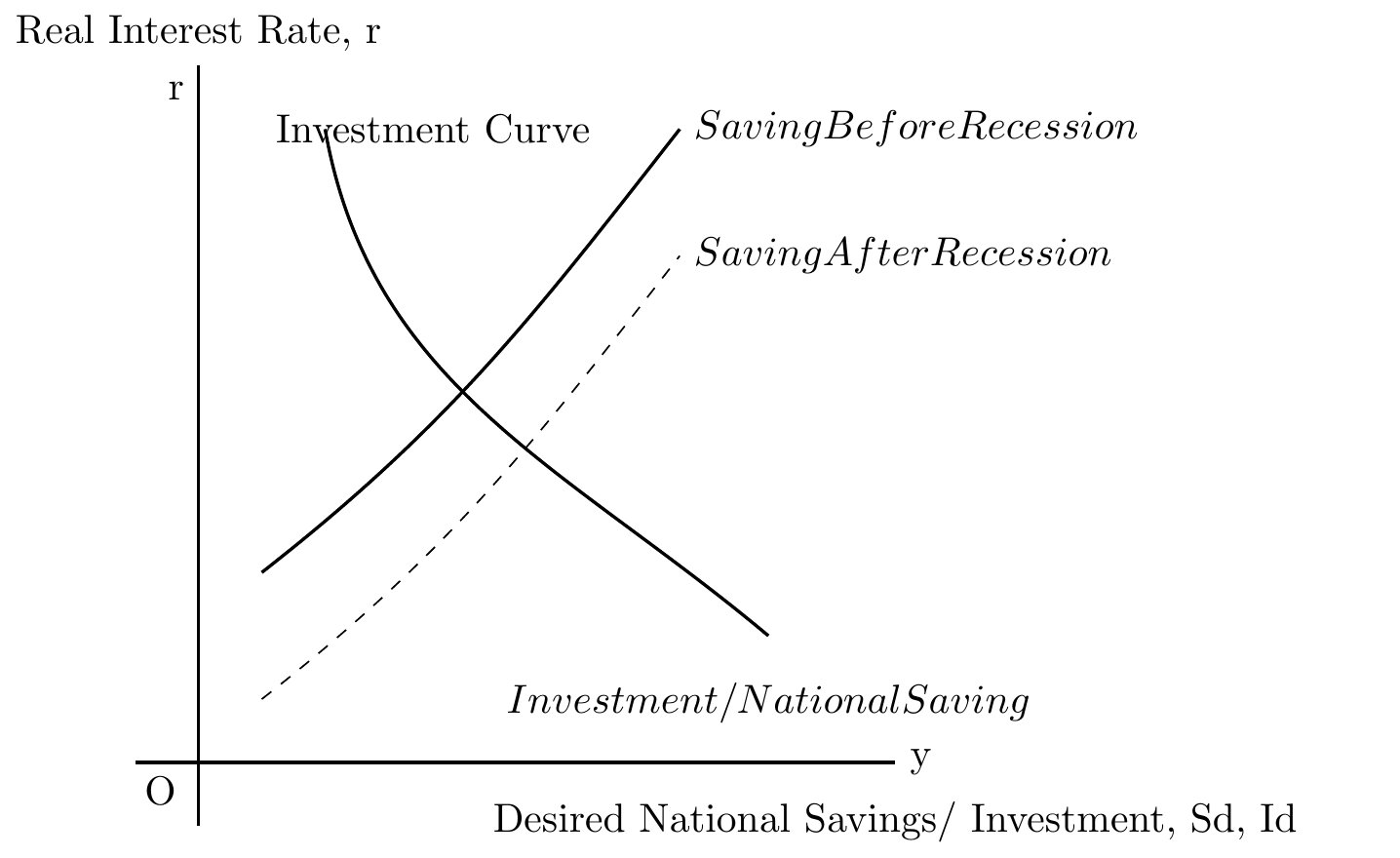
Future Oriented-Households
As consumers become more future orienting their saving rate increases.
As the volume of savings the savings curve will shift outward reflecting an increased supply of savings.
This will result in a new equilibrium point with the interest rate, which will reduce the equilibrium interest rate.
\begin{tikzpicture}[scale=1.1]
% Axis
\draw [thick] (-0.3,0) node [below] {O} (-0.5,0)-- (0,0) -- (5.5,0) node [right] {y};
\node [above] at (0,5.5) {Real Interest Rate, r};
\node [below] at (5.5,-0.2) {Desired National Savings/ Investment, Sd, Id};
\draw [thick] (0,-0.5)-- (0,0) -- (0,5.5);
\node [left] at (0,5.3) {r};
%Downward slopping line
\node [right] at (0.5,5) {Investment Curve};
\draw [thick] (1,5) to [out=280,in=140] (4.5,1);
\node [above] at (4.5,0.2) {$Investment/ National Saving$};
%Initial Savings
\draw [dashed] (0.5,0.5) to [out=38,in=232] (3.8,4);
\node [left] at (0.43,0.5) {};
\node [right] at (3.8,4) {$Saving After Recession$};
\draw [thick] (0.5,1.5) to [out=38,in=232] (3.8,5);
\node [left] at (0.43,0.5) {};
\node [right] at (3.8,5) {$Saving Before Recession$};
\end{tikzpicture}
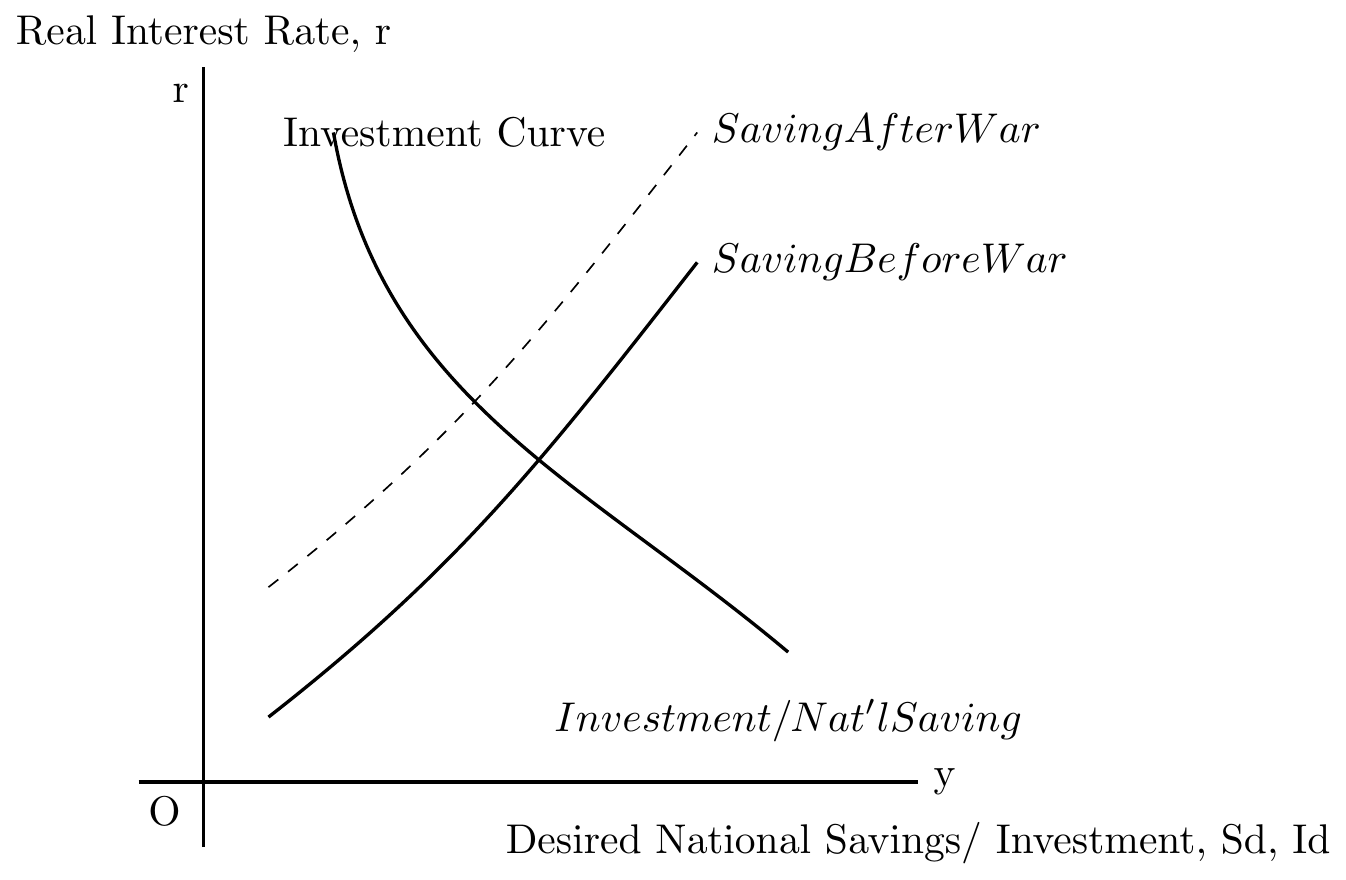
Government Spending
Should the government launch on a debit financed spending campaign, this new debt will shift the saving curve to the lft resulting in higher real interest rates and potentially crowding out private investment.
\begin{tikzpicture}[scale=1.1]
% Axis
\draw [thick] (-0.3,0) node [below] {O} (-0.5,0)-- (0,0) -- (5.5,0) node [right] {y};
\node [above] at (0,5.5) {Real Interest Rate, r};
\node [below] at (5.5,-0.2) {Desired National Savings/ Investment, Sd, Id};
\draw [thick] (0,-0.5)-- (0,0) -- (0,5.5);
\node [left] at (0,5.3) {r};
%Downward slopping line
\node [right] at (0.5,5) {Investment Curve};
\draw [thick] (1,5) to [out=280,in=140] (4.5,1);
\node [above] at (4.5,0.2) {$Investment/ Nat'l Saving$};
%Initial Savings
\draw [thick] (0.5,0.5) to [out=38,in=232] (3.8,4);
\node [left] at (0.43,0.5) {};
\node [right] at (3.8,4) {$Saving Before War$};
\draw [dashed] (0.5,1.5) to [out=38,in=232] (3.8,5);
\node [left] at (0.43,0.5) {};
\node [right] at (3.8,5) {$Saving After War$};
\end{tikzpicture}
LS0tCnRpdGxlOiBHcmFwaGluZyBTaG9ja3MgYW5kIEVxdWlsaWJyaXVtCmNvZGVfZm9sZGluZzogInNob3ciCi0tLQoKYGBge3IgZWNobz1GQUxTRSwgbWVzc2FnZT1GQUxTRSwgd2FybmluZz1GQUxTRX0Kc291cmNlKCJSL2hlbHBlcnMuUiIpCmxpYnJhcnkodGlkeXZlcnNlKQpsaWJyYXJ5KGZyZWRyKQpsaWJyYXJ5KG5vbW5vbWwpCmtuaXRyOjpvcHRzX2NodW5rJHNldCh3YXJuaW5nID0gRkFMU0UsIG1lc3NhZ2UgPSBGQUxTRSwgZmlnLmFsaWduID0gImNlbnRlciIsIG91dC53aWR0aCA9ICI4MCUiKQpgYGAKCiMgSW50cm9kdWN0aW9uCgpUaGlzIHNlY3Rpb24gbGlzdHMgc29tZSBleGFtcGxlcyBvZiBzaGlmdHMgaW4gdGhlIEdvb2QgTWFya2V0IEVxdWlsaWJyaXVtIGFzIHdlbGwgYXMgdGhlIGxhYm9yIG1hcmtldCBlcXVpbGlicml1bS4KCkFkZGl0aW9uYWxseSwgSSBhbSBsZWF2aW5nIG15IHRpa3ogY29kZS0tIHRoZXNlIHByb3ZpZGUgZGVjZW50IGV4YW1wbGVzIGZvciBtYWtpbmcgdGhlc2Uga2luZHMgb2YgZ3JhcGhzLgoKIyBTdXBwbHkgU2hvY2sgRXhhbXBsZQoKSW1hZ2luZSB0aGUgY29zdCBvZiBlbmVyZ3kgaW5jcmVhc2luZy4KVGhpcyByaXNpbmcgY29zdCB3b3VsZCBtYWtlIGVhY2ggd29ya2VyIGxlc3MgcHJvZHVjdGl2ZSBhdCBhbnkgbGV2ZWwgb2Ygb3V0cHV0IChzdXBwbHkgc2lkZSBzaG9jaykuClRoaXMgc3Vic2VxdWVudCByZWR1Y3Rpb24gb2YgdGhlIG1hcmdpbmFsIHByb2R1Y3Qgb2YgbGFib3Igd291bGQgc2hpZnQgdGhlIGVxdWlsaWJyaXVtIHN1Y2ggdGhhdCBmaXJtcyB3b3VsZCByZXF1aXJlIGxlc3Mgd29ya2VycyBpbiBvcmRlciB0byBhY2hpZXZlIGVxdWlsaWJpcml1bS4KCmBgYHtyLCBlbmdpbmU9J3Rpa3onLCBvdXQud2lkdGg9JzkwJScsIGZpZy5jYXA9J1N1cHBseSBTaG9jayBSZWR1Y2luZyBNUE4gQW5kIFRodXMgSW5jcmVhc2luZyBVbmVtcGxveW1lbnQgZnJvbSBOMSB0byBOMiBhbmQgRGVjcmVhc2luZyBSZWFsIFdhZ2VzIGZyb20gdzEgdG8gdzInfQpcYmVnaW57dGlrenBpY3R1cmV9W3NjYWxlPTFdCgolIEF4aXMKClxkcmF3IFt0aGlja10gKC0wLjMsMCkgbm9kZSBbYmVsb3ddIHtPfSAoLTAuNSwwKS0tICgwLDApIC0tICg1LjUsMCkgbm9kZSBbcmlnaHRdIHt5fTsKClxub2RlIFthYm92ZV0gYXQgKDAsNS41KSB7Q3VycmVudCBSZWFsIFdhZ2VzLCB3fTsKClxub2RlIFtiZWxvd10gYXQgKDUuNSwtMC4yKSB7TGFib3IsIE59OwoKXGRyYXcgW3RoaWNrXSAoMCwtMC41KS0tICgwLDApIC0tICgwLDUuNSk7Cgpcbm9kZSBbbGVmdF0gYXQgKDAsNS4zKSB7d307CgoKJURvd253YXJkIHNsb3BwaW5nIGxpbmUKClxub2RlIFthYm92ZV0gYXQgKDAuNSw1KSB7d307CgpcZHJhdyBbdGhpY2tdICgwLjUsNSkgdG8gW291dD0yODAsaW49MTQwXSAoNC41LDEpOwoKXG5vZGUgW2Fib3ZlXSBhdCAoNC41LDAuMikgeyRORDEkfTsKCiVEb3dud2FyZCBzbG9wcGluZyBsaW5lIGFmdGVyIHNob2NrCgpcbm9kZSBbYWJvdmVdIGF0ICgwLjUsNSkge3d9OwoKXGRyYXcgW3RoaWNrXSAoMC41LDMpIHRvIFtvdXQ9MjkwLGluPTEzMF0gKDMuNSwuNSk7Cgpcbm9kZSBbYWJvdmVdIGF0ICgzLDAuMSkgeyRORDIkfTsKCgolIFVwd2FyZCBTbG9wcGluZyBQUQoKXGRyYXcgW3RoaWNrXSAoMC4zLDAuNSkgdG8gW291dD0zOCxpbj0yMzJdICgzLjgsNCk7Cgpcbm9kZSBbbGVmdF0gYXQgKDAuNDMsMC41KSB7fTsKClxub2RlIFtyaWdodF0gYXQgKDMuOCw0KSB7JE5TJH07CgoKCiUgZGFzaGVkIGxpbmVzCgpcZHJhdyBbZGFzaGVkXSAoMCwyLjQpLS0oMi41LDIuNCk7Cgpcbm9kZSBbbGVmdF0gYXQgKDIuNSwtLjIpIHskTjEkfTsKCiUgTmV3IEVxdWlsaWJyaXVtClxkcmF3IFtkYXNoZWRdKDEuOCwwKS0tKDEuOCwxLjcpOwolIE9sZCBFcXVpbGlicml1bQpcZHJhdyBbZGFzaGVkXSgyLjUsMCktLSgyLjUsMi40KTsKClxkcmF3IFtkYXNoZWRdKDAsMS43KS0tKDEuOCwxLjcpOwoKXG5vZGUgW2xlZnRdIGF0ICgxLjgsLS4yKSB7JE4yJH07Cgpcbm9kZSBbbGVmdF0gYXQgKDAsMS43KSB7JHcyJH07Cgpcbm9kZSBbbGVmdF0gYXQgKDAsMi40KSB7JHcxJH07CgpcZW5ke3Rpa3pwaWN0dXJlfQpgYGAKCiMgRnV0dXJlIE9yaWVudGVkLUhvdXNlaG9sZHMKCkFzIGNvbnN1bWVycyBiZWNvbWUgbW9yZSBmdXR1cmUgb3JpZW50aW5nIHRoZWlyIHNhdmluZyByYXRlIGluY3JlYXNlcy4KQXMgdGhlIHZvbHVtZSBvZiBzYXZpbmdzIHRoZSBzYXZpbmdzIGN1cnZlIHdpbGwgc2hpZnQgb3V0d2FyZCByZWZsZWN0aW5nIGFuIGluY3JlYXNlZCBzdXBwbHkgb2Ygc2F2aW5ncy4KVGhpcyB3aWxsIHJlc3VsdCBpbiBhIG5ldyBlcXVpbGlicml1bSBwb2ludCB3aXRoIHRoZSBpbnRlcmVzdCByYXRlLCB3aGljaCB3aWxsIHJlZHVjZSB0aGUgZXF1aWxpYnJpdW0gaW50ZXJlc3QgcmF0ZS4KCmBgYHtyLCBlbmdpbmU9J3Rpa3onLCBvdXQud2lkdGg9JzkwJScsIGZpZy5jYXA9J1NoaWZ0IGluIFNhdmluZ3MgQ3VydmUgRHVlIHRvIFJlY2Vzc2lvbjogQXQgYW55IHZhbHVlIG5ldyB2YWx1ZSBvZiByLCBtb3JlIHByaXZhdGUgc2F2aW5nJ30KXGJlZ2lue3Rpa3pwaWN0dXJlfVtzY2FsZT0xLjFdCgolIEF4aXMKClxkcmF3IFt0aGlja10gKC0wLjMsMCkgbm9kZSBbYmVsb3ddIHtPfSAoLTAuNSwwKS0tICgwLDApIC0tICg1LjUsMCkgbm9kZSBbcmlnaHRdIHt5fTsKClxub2RlIFthYm92ZV0gYXQgKDAsNS41KSB7UmVhbCBJbnRlcmVzdCBSYXRlLCByfTsKClxub2RlIFtiZWxvd10gYXQgKDUuNSwtMC4yKSB7RGVzaXJlZCBOYXRpb25hbCBTYXZpbmdzLyBJbnZlc3RtZW50LCBTZCwgSWR9OwoKXGRyYXcgW3RoaWNrXSAoMCwtMC41KS0tICgwLDApIC0tICgwLDUuNSk7Cgpcbm9kZSBbbGVmdF0gYXQgKDAsNS4zKSB7cn07CgoKJURvd253YXJkIHNsb3BwaW5nIGxpbmUKXG5vZGUgW3JpZ2h0XSBhdCAoMC41LDUpIHtJbnZlc3RtZW50IEN1cnZlfTsKXGRyYXcgW3RoaWNrXSAoMSw1KSB0byBbb3V0PTI4MCxpbj0xNDBdICg0LjUsMSk7Clxub2RlIFthYm92ZV0gYXQgKDQuNSwwLjIpIHskSW52ZXN0bWVudC8gTmF0aW9uYWwgU2F2aW5nJH07CgolSW5pdGlhbCBTYXZpbmdzClxkcmF3IFtkYXNoZWRdICgwLjUsMC41KSB0byBbb3V0PTM4LGluPTIzMl0gKDMuOCw0KTsKXG5vZGUgW2xlZnRdIGF0ICgwLjQzLDAuNSkge307Clxub2RlIFtyaWdodF0gYXQgKDMuOCw0KSB7JFNhdmluZyBBZnRlciBSZWNlc3Npb24kfTsKClxkcmF3IFt0aGlja10gKDAuNSwxLjUpIHRvIFtvdXQ9MzgsaW49MjMyXSAoMy44LDUpOwpcbm9kZSBbbGVmdF0gYXQgKDAuNDMsMC41KSB7fTsKXG5vZGUgW3JpZ2h0XSBhdCAoMy44LDUpIHskU2F2aW5nIEJlZm9yZSBSZWNlc3Npb24kfTsKCgpcZW5ke3Rpa3pwaWN0dXJlfQoKCgpgYGAKCiMgR292ZXJubWVudCBTcGVuZGluZwoKU2hvdWxkIHRoZSBnb3Zlcm5tZW50IGxhdW5jaCBvbiBhIGRlYml0IGZpbmFuY2VkIHNwZW5kaW5nIGNhbXBhaWduLCB0aGlzIG5ldyBkZWJ0IHdpbGwgc2hpZnQgdGhlIHNhdmluZyBjdXJ2ZSB0byB0aGUgbGZ0IHJlc3VsdGluZyBpbiBoaWdoZXIgcmVhbCBpbnRlcmVzdCByYXRlcyBhbmQgcG90ZW50aWFsbHkgY3Jvd2Rpbmcgb3V0IHByaXZhdGUgaW52ZXN0bWVudC4KCmBgYHtyLCBlbmdpbmU9J3Rpa3onLCBvdXQud2lkdGg9JzkwJScsIGZpZy5jYXAgPSAnRGVidCBTaGlmdHMgdGhlIFNhdmluZyBDdXJ2ZSB0byB0aGUgTGVmdCBSZXN1bHRpbmcgaW4gSGlnaGVyIFJlYWwgSW50ZXJlc3QgUmF0ZXMgYW5kIENyb3dkaW5nIE91dCBQcml2YXRlIEludmVzdG1lbnQnfQpcYmVnaW57dGlrenBpY3R1cmV9W3NjYWxlPTEuMV0KCiUgQXhpcwoKXGRyYXcgW3RoaWNrXSAoLTAuMywwKSBub2RlIFtiZWxvd10ge099ICgtMC41LDApLS0gKDAsMCkgLS0gKDUuNSwwKSBub2RlIFtyaWdodF0ge3l9OwoKXG5vZGUgW2Fib3ZlXSBhdCAoMCw1LjUpIHtSZWFsIEludGVyZXN0IFJhdGUsIHJ9OwoKXG5vZGUgW2JlbG93XSBhdCAoNS41LC0wLjIpIHtEZXNpcmVkIE5hdGlvbmFsIFNhdmluZ3MvIEludmVzdG1lbnQsIFNkLCBJZH07CgpcZHJhdyBbdGhpY2tdICgwLC0wLjUpLS0gKDAsMCkgLS0gKDAsNS41KTsKClxub2RlIFtsZWZ0XSBhdCAoMCw1LjMpIHtyfTsKCgolRG93bndhcmQgc2xvcHBpbmcgbGluZQpcbm9kZSBbcmlnaHRdIGF0ICgwLjUsNSkge0ludmVzdG1lbnQgQ3VydmV9OwpcZHJhdyBbdGhpY2tdICgxLDUpIHRvIFtvdXQ9MjgwLGluPTE0MF0gKDQuNSwxKTsKXG5vZGUgW2Fib3ZlXSBhdCAoNC41LDAuMikgeyRJbnZlc3RtZW50LyBOYXQnbCBTYXZpbmckfTsKCiVJbml0aWFsIFNhdmluZ3MKXGRyYXcgW3RoaWNrXSAoMC41LDAuNSkgdG8gW291dD0zOCxpbj0yMzJdICgzLjgsNCk7Clxub2RlIFtsZWZ0XSBhdCAoMC40MywwLjUpIHt9Owpcbm9kZSBbcmlnaHRdIGF0ICgzLjgsNCkgeyRTYXZpbmcgQmVmb3JlIFdhciR9OwoKXGRyYXcgW2Rhc2hlZF0gKDAuNSwxLjUpIHRvIFtvdXQ9MzgsaW49MjMyXSAoMy44LDUpOwpcbm9kZSBbbGVmdF0gYXQgKDAuNDMsMC41KSB7fTsKXG5vZGUgW3JpZ2h0XSBhdCAoMy44LDUpIHskU2F2aW5nIEFmdGVyIFdhciR9OwoKClxlbmR7dGlrenBpY3R1cmV9CmBgYAo=
Code licensed under the BSD 3-clause license
Text licensed under the CC-BY-ND-NC 4.0 license
Copyright © 2020 Michael DeWitt